Leonardo da Pisa, auch Fibonacci genannt (* um 1180 in Pisa, † um 1241), ist der bedeutendste Mathematiker des Mittelalters. Über die Biographie Fibonacci’s ist nur wenig bekannt. Der Kaufmannsohn bereiste Nordafrika und Arabien und lernte nicht nur das Rechnen mit den neun indo-arabischen Ziffern, sondern auch die Null kennen. In Europa wurde zu dieser Zeit noch mit römischen Ziffern gerechnet, mit welchen keine höhere Mathematik möglich war – ein echter Hemmschuh für die Weiterentwicklung der Wissenschaften in der damaligen Zeit. In seinem Hauptwerk „Liber Abbaci“ (1202) stellte er der lateinisch sprechenden Welt die Vorzüge der neun indo-arabischen Ziffern und der Null vor und etablierte das noch heute verwendete Zahlensystem im mittelalterlichen Europa.
Die Fibonacci-Zahlenfolge ist eine mathematische Folge nicht negativer, ganzer Zahlen, die durch das rekursive Bildungsgesetz definiert wird:
- \( f_n = f_{n-1} + f_{n-2}\)
für
- \( {n \ge 2}\)
- \( f_0 = 0 \)
- \( f_1 = 1 \)
Die beiden ersten Zahlen 0 und 1 werden vorgegeben und jede weitere Zahl ist die Summe ihrer beiden Vorgänger.
0+1=1; 1+1=2; 1+2=3; 3+2=5; 5+3=8; 8+5=13; 13+8=21; 21+13=34 usw .….
Daraus ergibt sich die Folge 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987.…
Die Zahlenfolge hat interessante Eigenschaften:
Das Verhältnis einer Zahl zur nächst höheren Zahl beträgt rund 0,618. In eine simple Formel gepackt, sieht das so aus:
- \( \frac{n}{n+1}=0,618 \)
Der Quotient der Division (n/n+1) nähert sich der Zahl 0,618. In der der Mathematik wird das als Grenzwert oder Limes der Folge bezeichnet. Die mathematisch korrekte Formel für die Berechnung des Grenzwertes sieht folgendermaßen aus:
- \( \lim_{n\to\infty} \ \frac{a_n}{a_{n+1}} \)
Das Verhältnis einer Zahl zur nächst niedrigeren Zahl beträgt rund 1,618.
Der Kehrwert von 1,6180 ist 0,6180.
Das Verhältnis zwischen den jeweils übernächsten Zahlen beträgt rund 0,382 in aufsteigender und 2,618 in absteigender Richtung.
Je weiter die Reihe fortschreitet, desto mehr nähert sich dieses Verhältnis der Zahl Phi Φ, einer irrationalen Zahl mit dem Wert 1,618033988.…
Hinter Phi Φ verbirgt sich die „Goldene Zahl“, auch unter dem „goldenen Schnitt“ bekannt (siehe Abbildung 1). Das (kleine) phi φ = 0,618… ist der Kehrwert vom (großen) Phi Φ.
Beim goldenen Schnitt wird eine Strecke L so zweigeteilt, dass sich das größere Segment zum kleineren Segment so verhält wie die Summe aus beiden zum größeren Segment: a verhält sich zu b wie (a + b) zu a.
- \( \frac{a}{b}= \frac{a+b}{a} \)
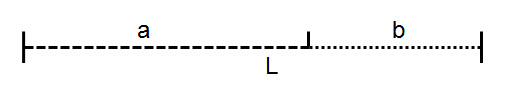
Der goldene Schnitt wird seit der Antike in der Architektur verwendet, ebenso in der Bildhauerei und Malerei.

Zurück zu den Fibo-Zahlen:
In einer kleinen Übersicht (Abbildung 2) dargestellt ergeben sich folgende Verhältnisse:
In dieser Tabelle (Abbildung 3) sind die Verhältnisse der Fibo-Zahlen berechnet. Die rot-gedruckten sind die wichtigsten.
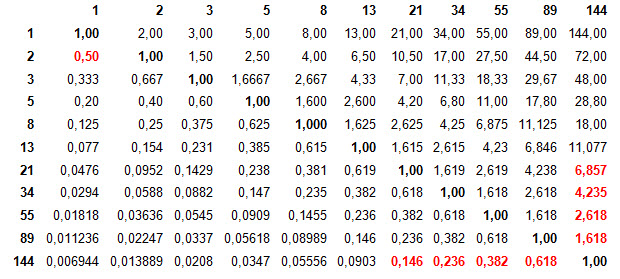
Hier nur einige Beispiele:
Bei einem Tannenzapfen oder einem Pinienzapfen, einer Ananas oder der Blüte einer Sonnenblume gibt es rechtsdrehende und linksdrehende, konzentrische Spiralen. Die Anzahl der Spiralen sind immer zwei Nachbarszahlen aus der Fibonacci Zahlenfolge. Der Aufbau der Schale eines Nautilus entspricht einer goldenen Spirale. Bei einer goldenen Spirale wird als Steigung das Teilungsverhältnis des goldenen Schnitts verwendet.
Verwendung von Fibonacci-Zahlen und Fibonacci-Verhältnissen in der Technischen Analyse
Zum einen werden die Fibonacci-Zahlen in vielfältiger Weise in der Technischen Analyse verwendet.
- Für die Einstellungen bei Indikatoren oder Oszillatoren werden Fibo-Zahlen verwendet:
- Statt eines 20er SMA's wird ein 21er verwendet.
- Beim MACD werden statt der Standardeinstellung (12, 26 und 9) die Perioden (21, 34 und 8) verwendet.
- Bei den Bollinger-Bändern werden statt einem 20er SMA und 2 Standardabweichungen ein 21er SMA und 1,618 Standardabweichungen verwendet.
In dieser kurzen Liste wurden nur wenige Beispiele genannt. Prinzipiell lässt sich jeder Indikator oder Oszillator mit Fibo-Zahlen modifizieren.
- Zum anderen werden die Fibonacci-Verhältnisse für die Bestimmung von Korrekturlevels und Kurszielen verwendet. Hintergrund dieser Überlegung ist, dass jede Trendbewegung irgendwann korrigiert wird. Ob das nun ein langfristiger, primärer Trend ist oder ein kurzfristiger, tertiärer Trend. Irgendwann setzt eine Korrekturbewegung ein und die Wahrscheinlichkeit, dass diese Korrektur bei einem Fibonacci-Verhältnis endet, ist recht groß.
- Die Korrekturlevels (= Retracements) sind die
- 23,6%
- 38,2%
- 50%
- 61,8%
- 78,6%
wobei die 38,2% und die 61,8% die relevantesten Korrekturlevels sind. Kritiker der Fibo-Verhältnisse führen immer an, dass die Levels nie exakt getroffen werden. Das ist sicher richtig - nur: Wenn wir eine Unterstützungs- oder Widerstandslinie einzeichnen, dann wird immer eine gewisse "Unschärfe" toleriert. Auch diese Linien werden selten exakt getroffen, sondern leicht unter- bzw. überschritten. Und was Unterstützungs- oder Widerstandslinien zugebilligt wird, sollte der Fairness halber auch Fibo-Korrekturlevels zugestanden werden.
Dies soll anhand von zwei Beispielen verdeutlicht werden.
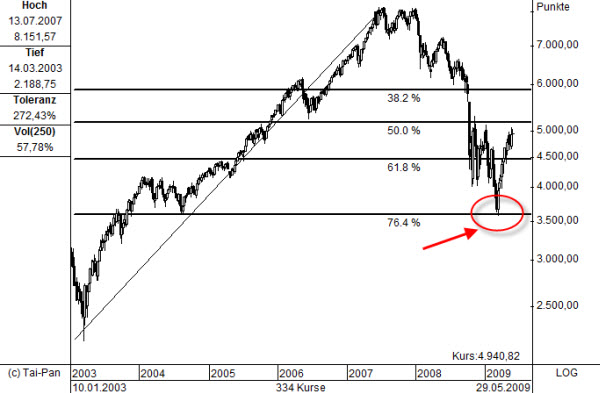
In Abbildung 4 der DAX, Wochenchart, 2003 bis 2009. Die Aufwärtsbewegung von März 2003 bis Juli 2007 wurde um ziemlich genau 76,4% bis März 2009 korrigiert.
In Abbildung 5 der EURUSD, Wochenchart, 2008 bis 2010. Die scharfe Abwärtsbewegung von Juli 2008 bis November 2008 wurde um 61,8% korrigiert.

Die Erweiterungen (= Extensions) sind die
-
- x 1,618
- x 2,618
- x 4,235
- x 6,857
wobei die 1,618 und die 2,618 die relevantesten Kursziele sind. Oder anderes ausgedrückt: 162% und 262%.
Zur Verdeutlichung ist die Kurszielberechnung mit Fibonacci-Extensions an einem Beispiel dargestellt, als „gemaltes“ Schema in Abbildung 6 und als „echtes“ Beispiel in Abbildung 7.
Zum Schema in Abbildung 6:

- Die Aufwärtsbewegung (von Punkt 1 nach Punkt 2) entspricht 100%.
- Diese Bewegung wird korrigiert (Punkt 2 nach Punkt 3).
- In der Regel endet die Korrektur an einem Fibonacci-Korrekturlevel.
- Nach Punkt 3 wird die Aufwärtsbewegung wieder aufgenommen.
- Für die Berechnung des Kurzieles werden 162% der ursprünglichen Aufwärtsbewegung (von Punkt 1 nach Punkt 2) an Punkt 3 nach oben abgetragen.
- In einem Abwärtstrend gilt das vice versa.

- Punkt 1 = 1,1874
- Punkt 2 = 1,2484
- Punkt 3 = 1,2149 (die Aufwärtsbewegung wurde damit um 50% korrigiert)
- 100% = 0,061 Pips (1,2484 – 1,1874)
- 162% = 0,099 Pips (0,061 * 1,62)
- 262% = 0,1598 Pips (0,061 * 2,62)
- Kursziel 1 = Punkt 3 + 162% = 1,3139 (1,2149 + 0,099)
- Kursziel 2 = Punkt 3 + 262% = 1,3747 (1,2148 + 0,1598)
An dieser Bewegung lässt sich die Herkunft dieser Variante 1 der Kurszielbestimmung erkennen: Elliott-Waves. Die Bewegung in EURUSD vom Juni 2010 bis Anfang Oktober 2010 entspricht einem 5-teiligen Impuls. Die Welle 3 erreicht in der Regel 162% Ausdehnung der Welle 1. Welle 3 wurde in diesem konkreten Beispiel um 62% korrigiert, Welle 5 erreichte dann 100% von Welle 3. Aufgrund der Verhältnistreue der Fibonacci-Extensions erreicht die Aufwärtsbewegung 262% von Welle 1.
